El Teorema de Norton

El Teorema de Norton  para circuitos eléctricos es dual del teorema de Thévenin. Se conoce así en honor al ingeniero Edward Lawry Norton, de los Laboratorios Bell, que lo publicó en un informe interno en el año 1926.​ El alemán Hans Ferdinand Mayer llegó a la misma conclusión de forma simultánea e independiente.

Establece que cualquier circuito lineal se puede sustituir por una fuente equivalente de intensidad en paralelo con una impedancia equivalente.

Al sustituir un generador de corriente por uno de tensión, el borne positivo del generador de tensión deberá coincidir con el borne positivo del generador de corriente y viceversa.

Calculo del circuito de Norton Equivalente 

El circuito Norton equivalente consiste en una fuente de corriente I_No en paralelo con una resistencia R_No. Para calcularlo:

1. Se calcula la corriente de salida, I_AB, cuando se cortocircuita la salida, es decir, cuando se pone una carga (tensión) nula entre A y B. Al colocar un cortocircuito entre A y B toda la intensidad I_No circula por la rama AB, por lo que ahora I_AB es igual a I_No.
2. Se calcula la tensión de salida, V_AB, cuando no se conecta ninguna carga externa, es decir, cuando se pone una resistencia infinita entre A y B. R_No es ahora igual a V_ABdividido entre I_No porque toda la intensidad I_No ahora circula a través de R_No y las tensiones de ambas ramas tienen que coincidir ( V_AB = I_NoR_No ).

Ejemplo de un circuito Norton Equivalente

Ejemplo 1

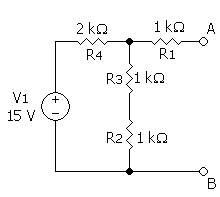
En el ejemplo, I_total viene dado por:

Usando la regla del divisor, la intensidad de corriente eléctrica tiene que ser:

Y la resistencia Norton equivalente sería:

Por lo tanto, el circuito equivalente consiste en una fuente de intensidad de 3.75mA en paralelo con una resistencia de 2 kΩ.

Ejemplo 2

Cortocircuitar las fuentes y eliminar la resistencia que hay entre los terminales para hallar Rs

Si ponemos a 0 V (en corto) las dos fuentes de tensión y los terminales A y B los ponemos en circuito abierto, vemos que las dos resistencias se conectan en paralelo.

El valor de la resistencia interna Rs se obtiene calculando la resistencia total en los terminales A y B dándonos el siguiente circuito:

Rs = (10 * 20) / (10 + 20)

Rs = 6.67 Ω

Conociendo la corriente de cortocircuito IS y la resistencia equivalente Rs, podemos montar el circuito equivalente de Norton:

El siguiente paso será resolver el problema con la resistencia de carga original de 40 Ω y así poder ver la caída de tensión A-B y la corriente que circula por RL.

---

Calcular la resistencia total (RT) calculando el paralelo de las dos resistencias:

RT = (40 * 6.67) / (40 + 6.67)

RT = 5.72 Ω

---

Hallar la caída de tensión entre A y B (VAB), es decir, la caída de voltaje en RL:

VAB = IS * RT

VAB = 2 * 5.72

VAB = 11.44 V

---

Finalmente calcular la corriente que circula por RL:

IL = VAB / RL

IL = 11.44 / 40

IL = 0.286 A