Teorema de Thévenin establece que si una parte de un circuito eléctrico lineal está comprendida entre dos terminales A y B, esta parte en cuestión puede sustituirse por un circuito equivalente que esté constituido únicamente por un generador de tensión en serie con una impedancia de forma que al conectar un elemento entre las dos terminales A y B, la tensión que cae en él y la intensidad que lo atraviesa son las mismas tanto en el circuito real como en el equivalente. El teorema de Thévenin es el dual del Teorema de Norton.
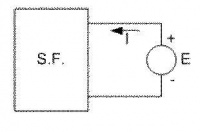
Es uno de los más importantes y de mayor aplicación. Sea un circuito lineal, en el que puede haber de todo, R, L, C, M, fuentes de tensión y corriente, independientes y dependientes. Distinguimos dos bornes A y B de ese circuito y conectamos una impedancia exterior Z
Se trata de calcular la corriente que circula por esa impedancia, sin resolver todo el circuito. Hacemos una hipótesis más: no hay mutua entre Z y el resto del circuito
1. Voltaje de Vacío o de Circuito Abierto: VAB Es el voltaje que aparece entre A y B cuando no existe la impedancia Z Es el que mediría un voltímetro "ideal" (ideal en el sentido de que al conectarse no modifica el voltaje que existía antes entre esos puntos. Ya precisaremos lo que esto significa). En Laplace, el voltaje de vacío será VAB(s).
2. Impedancia Vista: ZAB Para definirla, anulemos todas las fuentes. Queda un circuito "pasivo" (mejor dicho: sin fuentes) ¿Qué quiere decir "anular las fuentes"? Las fuentes de tensión se cortocircuitan; las de corriente se abren. ¿Cuáles? Las independientes y datos previos; no así las dependientes que no son generadores sino vínculos. Una vez anuladas las fuentes, aplicamos una fuente de tensión E entre A y B.
Circula una corriente I. El cociente E/ I, que no depende de E, debido a la linealidad del circuito ya que E es la única fuente, es lo que se llama impedancia vista. ZAB(s) = E(s)/ I (s) E(s) es cualquiera; no la especificamos. En casos sencillos, no hace falta calcular ZAB; alcanza con "mirar" desde A y B, y reconocer una combinación (por ejemplo series y/o paralelos) de impedancias sencillas. Hay pues, dos métodos para calcular ZAB: la definición o "mirar".
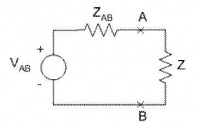
"La corriente que pasa por la impedancia Z conectada entre los bornes A y B es I = VAB/)ZAB+Z)"
Es decir que independientemente de lo que haya dentro de la "caja negra", si conocemos esos dos parámetros VAB y ZAB, estamos en condiciones de saber qué corriente va a pasar por cualquier Z En particular, si cortocircuitamos A y B tenemos una corriente que denominamos de cortocircuito: Icc = VAB/ZAB
Demostración
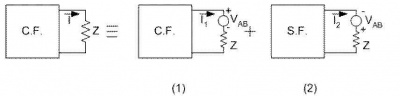
Se apoya en la linealidad del circuito, que nos permite aplicar superposición. Superpondremos dos estados de modo de obtener el circuito original.
Al superponer, las fuentes se van y queda el circuito original. La configuración interna de la caja negra es la misma -salvo la anulación de las fuentes en (2) Entonces: I = I1 + I2 En el circuito (1), recordando la definición de VAB, digo que I1 = 0 es solución (desde el punto de vista de la caja negra, está "abierta" : pareja compatible I1 = 0 voltaje VAB y desde el punto de vista de la carga también es compatible, porque con I1 = 0, no hay caída en Z - si no hay mutua-) Aceptando unicidad de la solución I1 = 0 Esto siempre que no haya mutua entre Z y el interior del circuito, pues si la hay, el voltaje entre A y B cambiaría. En el circuito (2) , recordando la definición de ZAB, es claro que I2 = VAB/(ZAB +Z )
Entonces: a los efectos de lo que pasa en Z, podemos reemplazar la caja negra por su equivalente Thévenin: fuente VAB e impedancia ZAB
¿Por qué? Pues en este también: I = VAB/(ZAB +Z)
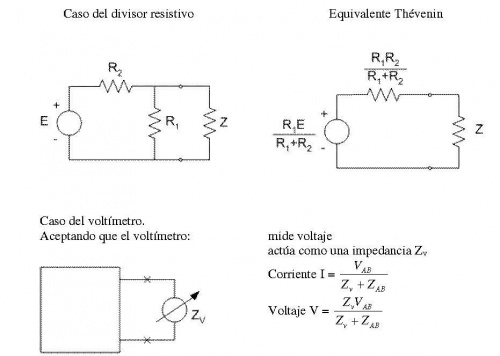
Para que el voltímetro mida VAB, es decir, para que al conectarlo no se altere el voltaje, debería ser Zv = ¥. En rigor, Zv >> ZAB Se dice que el voltímetro no "carga" al resto del circuito. En los testers comunes (analógicos), la Zv se da en W/V, p.ej. 10k/V. Quiere decir que en la escala de 10V, Zv = 10x10 = 100k . Si lo conectamos en un circuito con una Z vista de 1k, el error cometido por el hecho de medir es del 1%. Si la Z vista fuera de 100k, se debe recurrir a otro tipo de voltímetro (digital, p.ej.) que presente una más alta impedancia propia.
Corriente de cortocircuito
Ya vimos que si cortocircuitamos A y B: Icc = VAB/ZAB Esto en particular sugiere otro método para calcular la impedancia vista. Hasta ahora vimos dos:
- Poner una fuente exterior, que llamamos E, anular las fuentes internas, y calcular E/ I
- Simplemente "mirar" desde A y B.
- Si conocemos VAB e Icc, es ZAB = VAB/Icc
Calculo de la tension de Thevenin
Para calcular la tensión de Thévenin, Vth, se desconecta la carga (es decir, la resistencia de la carga) y se calcula VAB. Al desconectar la carga, la intensidad que atraviesa Rth en el circuito equivalente es nula y por tanto la tensión de Rth también es nula, por lo que ahora VAB = Vth por la segunda ley de Kirchhoff.
Debido a que la tensión de Thévenin se define como la tensión que aparece entre los terminales de la carga cuando se desconecta la resistencia de la carga también se puede denominar tensión en circuito abierto.
Para calcular la resistencia de Thévenin, se desconecta la resistencia de carga, se cortocircuitan las fuentes de tensión y se abren las fuentes de corriente. Se calcula la resistencia que se ve desde los terminales AB y esa resistencia RAB es la resistencia de Thevenin buscada Rth = RAB
Ejemplo
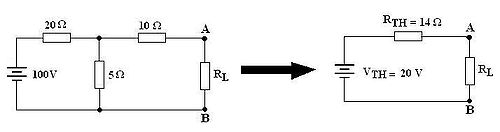
En primer lugar, se calcula la tensión de Thévenin entre los terminales A y B de la carga; para ello, se desconecta RL del circuito (queda un circuito abierto entre A y B). Una vez hecho esto, podemos observar que la resistencia de 10 Ω está en circuito abierto y no circula corriente a través de ella, con lo que no produce ninguna caída de tensión. En estos momentos, el circuito que se necesita estudiar para calcular la tensión de Thévenin está formado únicamente por la fuente de tensión de 100 V en serie con dos resistencias de 20 Ω y 5 Ω. Como la carga RL está en paralelo con la resistencia de 5 Ω (recordar que no circula intensidad a través de la resistencia de 10 Ω), la diferencia de potencial entre los terminales A y B es igual que la tensión que cae en la resistencia de 5 Ω (ver también Divisor de tensión), con lo que la tensión de Thévenin resulta:
Para calcular la resistencia de Thévenin, se desconecta la carga RL del circuito y se anula la fuente de tensión sustituyéndola por un cortocircuito. Si se colocara una fuente de tensión (de cualquier valor) entre los terminales A y B, veríamos que las tres resistencias soportarían una intensidad. Por lo tanto, se halla la equivalente a las tres: las resistencias de 20 Ω y 5 Ω están conectadas en paralelo y estas están conectadas en serie con la resistencia de 10 Ω, entonces:


No comments:
Post a Comment